西暦2000年は「400年に一度の特別なうるう年」だ。なぜ、うるう年の規則は、そんなに複雑な

のだろう。

　地球の公転周期と自転周期の比、という問題の本質にさかのぼって、そもそもうるう年とは

何か考えてみよう。

　西暦年数が４で割り切れる年は、うるう年で、2月が29日まである。ただし、例外として、西暦

年数が100で割り切れる年は、４で割り切れるけれど、平年とする。さらに、例外中の例外とし

て、西暦年数が400で割り切れる年は、100で割り切れるけれど、うるう年とする。

　以上が現在の暦法である「グレゴリオ暦」のシステム。要するに、400年につき97回のわりあ

いで、うるう年を置く。西暦1900年や2100年は、グレゴリオ暦では平年だが、今年、西暦2000

年は、うるう年となる。

　日常生活に用いる暦は、一年が四季の一巡の周期と合っていると、べんりだ。

　これは、地球が太陽のまわりを一巡する周期、つまり地球の公転周期（正確には「回帰年」）

と関係している。

　ほかの暦法として、月の満ち欠けの周期を用いるイスラム暦のようなものもある。この場合、

暦の月と四季の関係は一定していない。

　「一日」というのは、基本的には、地球の自転周期だ。地球の自転と公転は、互いに別の現

象なので、これらふたつの周期は複雑な関係になる。

　具体的に、現在、回帰年は約365.2422日という、複雑な端数のつく値になっている。もし暦の

一年を365日に固定したらどうだろう。四季が一巡するのに365.2422日かかるのに、カレンダは

365日周期で進む。

　一年につき0.2422日ずつ、カレンダの日付が実際の四季よりどんどん先に進んでしまう。こ

の差は４年で約１日となり、400年後にはカレンダと実際の季節の関係が100日もずれてしま

う。これは、かなりまずい。

　だから、おおざっぱに、４年に一度、うるう年を置いて、カレンダの日付を一日「足踏み」させ

て待たせる。ここで、四季のリズムは、進みすぎているカレンダの日付に追いつけるわけだ。こ

の「４年に一度のうるう年」が現在の西暦のもととなっているユリウス暦のシステムだ。

　ユリウス暦の一年は、平均365.25日である。これは実際の回帰年より0.0078日、長すぎる。

ユリウス暦を長期間つづけていると、だんだんカレンダの日付が四季のリズムに対して遅れて

くる。そこで、少しうるう年の頻度を減らして、カレンダのもたつきを解消することが考えられる。

これがグレゴリオ暦で、公式には、西暦1582年にユリウス暦から切り替わった。

　そのさい、ユリウス暦1582年10月4日の翌日をグレゴリオ暦1582年10月15日とした。日付を

10日間も飛ばしたわけだが、そのくらいカレンダが実際の季節に比べて遅れていたわけで、ま

た、だからこそ、改暦が必要になったといえる。グレゴリオ暦の一年は、平均すると

(400 x 365 + 97)/400 = 365.2425 [日]

となるが、これは、実際の回帰年とほぼ等しい。

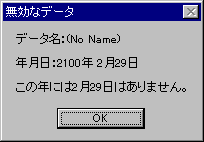
　アストロロギアは、以上すべてのことを正しく認識し、例えば西暦2100年には2月29日がない

ことを知っている（上の画像参照）。また、1582年の改暦にも対応しており、この年の10月4日

の翌日は15日だと知っている。

　1582年10月5日などを指定しようものなら「その日付は存在しない」というエラーメッセージを

出す。けれど、すべてのソフトがそこまで徹底して暦法を知っているわけでは、ないだろう。